合肥
转眼到了24年，23年过的很快，对23年进行一个简单的总结，再期待下24年吧

23年的过往

  • 工作：按部就班，没有一些积极的事情发生，还是欠缺很多思考
  • 跑步：全年1100km，参加两场马拉松，也是取得了个人突破
  • 总结能力：还是依然不足，需要再看看类似于金字塔原理之类的书
  • 旅行：
    • 清明：长沙、武汉，长沙的笨萝卜很赞
    • 端午：重庆，渝大狮火锅很赞
    • 国庆：榆林和延安，陕北远比我想象中发展的要好很多，但是依然很多地方贫穷，老年留守人口居多
    • 冬天：去合肥看了人生第一场演唱会，伍佰还是那么富有感染力；随后去了南京，很喜欢南方的秋冬，小厨娘好评

24年的目标

  • 学习：学日语，学rust(做一个小的项目)
  • Coding：GitHub 10个pr 至少
  • 投资：收益A股10% 美股10%
  • 旅游：带父母去趟日本，再解锁一些南方城市吧
  • 读书：带笔记的读完10本书
  • 运动：两场马拉松

.bash_profile vs .bashrc
在使用Linux的时候，我们经常设置环境变量，.bash_profile和.bashrc文件都可以用来设置，那么两者到底有什么区别

1. Interactive Login和Non-Login Shell

  • Interactive Shell: a shell that reads and writes to a user’s terminal
  • Non-interactive Shell: a shell that is not associated with a terminal, like when executing a script.

1.1 Interactive Shell

An interactive shell can be either login or non-login shell.

  • login shell: A login shell is invoked when a user login to the terminal either remotely via ssh or locally, or when Bash is launched with the --login option
  • non-login shell: An interactive non-login shell is invoked from the login shell, such as when typing bash in the shell prompt or when opening a new Gnome terminal tab.

1.2 Bash Startup Files

When invoked as an interactive login shell, Bash looks for the /etc/profile file, and if the file exists , it runs the commands listed in the file. Then Bash searches for ~/.bash_profile, ~/.bash_login, and ~/.profile files, in the listed order, and executes commands from the first readable file found.

When Bash is invoked as an interactive non-login shell, it reads and executes commands from ~/.bashrc, if that file exists, and it is readable.

1.3 做个实验

给Shell1中设置一个alias

1
2
3
4
[toni@os ~/workpalce/pay_otel]$ echo "alias gitst='git status'" >> ~/.bashrc 
[toni@os ~/workpalce/pay_otel]$ gitst
Hey! No command 'gitst' found, did you mean 'dist'?
[toni@os ~/workpalce/pay_otel]$

设置完后立刻打开一个新的Shell，可以看到设置的alias是立刻剩下的，说明.bashrc是interactive non-login shell会读取的

1
2
3
4
5
6
7
8
9
10
11
[toni@os ~/workpalce/pay_otel]$ gitst
On branch master
Your branch is up to date with 'origin/master'.

Changes not staged for commit:
  (use "git add <file>..." to update what will be committed)
  (use "git restore <file>..." to discard changes in working directory)
        modified:   dtools.sh
        modified:   pay_otel.go

no changes added to commit (use "git add" and/or "git commit -a")

2. .bashrc与.bash_profile的区别

  • .bash_profile is read and executed when Bash is invoked as an interactive login shell, while .bashrc is executed for an interactive non-login shell
  • Use .bash_profile to run commands that should run only once, such as customizing the $PATH environment variable .
  • Put the commands that should run every time you launch a new shell in the .bashrc file. This include your aliases and functions , custom prompts, history customizations , and so on.
  • Typically, ~/.bash_profile contains lines like below that source the .bashrc file. This means each time you log in to the terminal, both files are read and executed.
1
2
3
if [ -f ~/.bashrc ]; then
	. ~/.bashrc
fi

Most Linux distributions are using ~/.profile instead of ~/.bash_profile. The ~/.profile file is read by all shells, while ~/.bash_profile only by Bash.

3. 参考

  1. .bash_profile vs .bash_rc

技术研究 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
message Expression {
    MetaInfo metaInfo = 1;    
    ExpressionType type = 2;
    // 值表达式
    Value valExpr = 3;
    // 计算表达式
    CalcExpression calcExpr = 4;
    // 逻辑表达式
    LogicExpression logicExpr = 5;
    // 关系表达式
    RelationExpression relationExpr = 6;
    // 函数表达式
    FuncExpression funcExpr = 7;
}

message CalcExpression {
    MetaInfo metaInfo = 1;    
    CalcExpressionType type = 2;
    CalcExpression left = 3;
    CalcExpression right = 4;
    Value value = 5;
    FuncExpression func = 6;
}

message RelationExpression {
    MetaInfo metaInfo = 1;    
    RelationExpressionType type = 2;
    CalcExpression left = 3;
    CalcExpression right = 4;
}

技术研究

Install minikube

安装minikube，参考 https://minikube.sigs.k8s.io/docs/start/

Start minikube

启动minikube，driver我们选择docker

1
[echo@echo] minikube start --driver=docker

Interact with your cluster

1
2
3
4
5
6
7
8
9
[echo@echo] kubectl get po -A
NAMESPACE     NAME                               READY   STATUS    RESTARTS      AGE
kube-system   coredns-565d847f94-b8swq           1/1     Running   2 (62s ago)   26m
kube-system   etcd-minikube                      1/1     Running   2 (67s ago)   26m
kube-system   kube-apiserver-minikube            1/1     Running   1 (68s ago)   26m
kube-system   kube-controller-manager-minikube   1/1     Running   2 (67s ago)   26m
kube-system   kube-proxy-859rk                   1/1     Running   2 (67s ago)   26m
kube-system   kube-scheduler-minikube            1/1     Running   2 (67s ago)   26m
kube-system   storage-provisioner                1/1     Running   3 (61s ago)   26m
1
2
3
4
5
6
7
8
9
[echo@echo] kubectl get po -A
NAMESPACE     NAME                               READY   STATUS    RESTARTS      AGE
kube-system   coredns-565d847f94-b8swq           1/1     Running   2 (62s ago)   26m
kube-system   etcd-minikube                      1/1     Running   2 (67s ago)   26m
kube-system   kube-apiserver-minikube            1/1     Running   1 (68s ago)   26m
kube-system   kube-controller-manager-minikube   1/1     Running   2 (67s ago)   26m
kube-system   kube-proxy-859rk                   1/1     Running   2 (67s ago)   26m
kube-system   kube-scheduler-minikube            1/1     Running   2 (67s ago)   26m
kube-system   storage-provisioner                1/1     Running   3 (61s ago)   26m
1
2
3
[echo@echo] kubectl create deployment hello-minikube --image=kicbase/echo-server:1.0

deployment.apps/hello-minikube created
1
2
3
[echo@echo] kubectl expose deployment hello-minikube --type=NodePort --port=8080

service/hello-minikube exposed
1
2
3
4
[echo@echo] kubectl get services hello-minikube

NAME             TYPE       CLUSTER-IP      EXTERNAL-IP   PORT(S)          AGE
hello-minikube   NodePort   10.107.69.159   <none>        8080:30227/TCP   9s
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
[echo@echo] minikube service hello-minikube

|-----------|----------------|-------------|---------------------------|
| NAMESPACE |      NAME      | TARGET PORT |            URL            |
|-----------|----------------|-------------|---------------------------|
| default   | hello-minikube |        8080 | http://192.168.49.2:30227 |
|-----------|----------------|-------------|---------------------------|
🏃  Starting tunnel for service hello-minikube.
|-----------|----------------|-------------|------------------------|
| NAMESPACE |      NAME      | TARGET PORT |          URL           |
|-----------|----------------|-------------|------------------------|
| default   | hello-minikube |             | http://127.0.0.1:52191 |
|-----------|----------------|-------------|------------------------|
🎉  正通过默认浏览器打开服务 default/hello-minikube...
❗  Because you are using a Docker driver on darwin, the terminal needs to be open to run it.

技术研究

参考文献

Go内存分配原则

  • Sharing down typically stays on the stack
    • 在调用方创建的变量或对象，通过参数的形式传递给被调用函数，这时，在调用方创建的内存空间通常在栈上。这种在调用方创建内存，在被调用方使用该内存的“内存共享”方式，称之为 Sharing down。
  • Sharing up typically escapes to the heap
    • 在被调用函数内创建的对象，以指针的形式返回给调用方的情况下，通常，创建的内存空间在堆上。这种在被调用方创建，在调用方使用的“内存共享”方式，称之为 Sharing up。
  • Only the compiler knows
    • 之所以上面两条原则都加了通常，因为具体的分配方式，是由编译器确定的，一些编译器后端优化，可能会突破这两个原则，因此，具体的分配逻辑，只有编译器（或开发编译器的人）知道。

堆分配内存的GC问题

  • Golang GC

技术研究

雪地

RDD介绍

Spark 的核心是建立在统一的抽象弹性分布式数据集（Resiliennt Distributed Datasets，RDD）之上的，这使得 Spark 的各个组件可以无缝地进行集成，能够在同一个应用程序中完成大数据处理。RDD 是 Spark 提供的最重要的抽象概念，它是一种有容错机制的特殊数据集合，可以分布在集群的结点上，以函数式操作集合的方式进行各种并行操作。

RDD的4大属性

  • partitions: 数据分片
  • partitioner: 分片切割原则
  • dependencies: RDD依赖
  • compute: 转换函数

阅读更多

布隆过滤器一种空间数据结构，用来判断一个元素是否在某个集合中。由于具有假阳性，所以布隆过滤器只能得出某个元素有可能在该集合，反之该元素一定不在这个集合中。

布隆过滤器简介

一个空的布隆过滤器是一个\(m\)位均为\(0\)的比特位数组，同时定义了\(k\)个哈希函数，将某个元素得出的哈希值映射到m个比特位中的某一位，将该为置为1，生成一个随机的分布。通常\(k\)要远远小于\(m\)，\(k\)和\(m\)的选取取决于过滤器的假阳性概率。

添加元素

当给布隆过滤器中添加一个元素时，利用\(k\)个哈希函数得出\(k\)个位置，并将\(m\)个比特位中对应的\(k\)个位置设置为\(1\)。

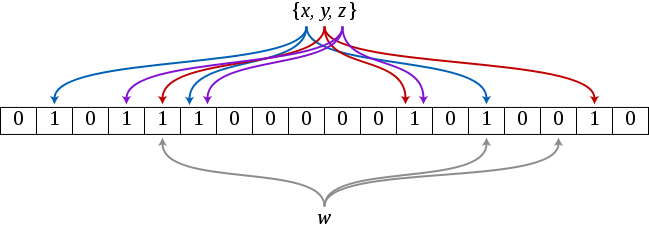
查询元素

查询元素时同样计算出\(k\)个位置，并获取该\(k\)个位置的所有元素值，当有一个位为\(0\)的话，就证明该元素不在该集合里。若\(k\)个位置均为\(1\)，则表示该元素可能在集合里，因为某些为\(1\)的位可能是别的元素在插入时设置的。

删除元素

由于假阳性的引入，布隆过滤器是不能删除元素的。

布隆过滤器的优点

链表、哈希表和平衡二叉树都能够做元素的查找，但是布隆过滤器明显在时间和空间利用率上更优

空间利用率

一个拥有1%的错误率和一个优化后的\(k\)的布隆过滤器，存储一个元素只需要\(9.6\)bit，没降低\(1%\)的错误率每个元素也只需增加\(4.8\)bit [文章中写的结论，还需要看证明过程]

时间复杂度

时间复杂度显然是\(O(k)\)

假阳性的概率

假定一个哈希函数选择每个插入位置的概率都是相等的，且位数组一共\(m\)位，那么某个比特位被hash函数不设为1的概率为
$$ 1 - \frac{1}{m}$$
那么通过计算k个哈希函数后，该位不被置为1的概率为
$$ ( 1 - \frac{1}{m} )^k$$
如果该过滤器有n个元素，那么该位为0的概率为
$$ ( 1 - \frac{1}{m} )^{kn}$$
该位为1的概率为
$$ 1- ( 1 - \frac{1}{m} )^{kn}$$
那么随便找k个位置，这些位置都为1的概率(也可认为是假阳性概率)为
$$ (1- ( 1 - \frac{1}{m} )^{kn})^k \approx (1 - e^{-kn/m})^k$$
需要注意的是，该概率不是严格准确的，因为\(k\)个为在被置1时，不是独立事件，但是概率大约是相似的。由此可见，假阳性的概率随着比特位数组长度\(m\)的增大而减小，随着集合元素\(n\)的增大而增大。那么证明了如果\(m\)足够大，布隆过滤器的准确性还是很高的。

如何寻找最适合的k

最适合的\(k\)就是能够使过滤器假阳性的概率达到最低，直观来讲增加哈希函数可以提升准确率，但是又会影响更多的比特位，所以随着哈希函数数量k的增加，假阳性概率或许增加或许减少，因此怎么算最适合的k呢。我们拿出上述得到的概率，假定假阳性概率为\(f\)

$$ f = (1 - e^{-kn/m})^k$$
为了简化运算对$f$取对数
$$ g = ln(f) = k*ln(1 - e^{-kn/m})$$
对其进行求导
$$\frac{dg}{dk} = ln(1 - e^{-kn/m}) + \frac{kn}{m} \frac{e^{-kn/m}}{1 - e^{-kn/m}}$$
当导数为0的时候，就是最适合的k，我们得出最适合的k如下:
$$ k = \frac{m}{n}ln(2) $$

元素数量估算

Swamidass & Baldi提出了布隆过滤器中实际元素估算的方式
$$ n^* = - \frac{mln[1-\frac{X}{k}]}{m} $$

其中，\(n^*\)为元素个数的近似值，\(m\)是位数组长度，\(k\)是哈希函数的数量, \(X\)是位数组中被置为1的位的数量。还没有看完证明过程

总结

布隆过滤器由于引入了假阳性，因此不太适合高精度的需求，业务场景需要能够接受一定错误容忍度，但是查询和插入都是\(O(k)\)的时间复杂度，空间复杂度也相当可观，因此在快速的元素查找定位场景还是大有裨益的。

参考文献

Bloom_filter
Notes 10 for CS 170
Mathematical Correction for Fingerprint Similarity Measures to Improve Chemical Retrieval

技术研究

故宫角楼

本文参考Mysql官方文档

共享锁和排它锁

  • 共享锁（shared locks：s lock）
  • 排它锁（exclusive locks：x lock）

意向锁（intention locks）- 表级别

  • 共享意向锁（intention shared lock -> IS）
  • 排他意向锁（intention exclusive lock -> IX）

意向锁与行锁间的关系

X IX S IS
X Conflict Conflict Conflict Conflict
IX Conflict Compatible Conflict Conflict
S Conflict Conflict Compatible Compatible
IS Conflict Compatible Compatible Compatible

意向锁注意事项

  • 事务申请一个表中某行记录的共享锁前，必须申请该表的IS lock或更强的锁
  • 事务申请一个表中某行记录的排他锁前，必须申请该表的IX lock
  • 意向锁只阻塞表级别的加锁请求（for example, LOCK TABLES ... WRITE)。意图锁主要是为了表明某些客户端正在或将要锁住表中的某一行。

记录锁(record lock)

记录锁也叫做行锁，是用来在一条索引记录上加锁来实现。例如SELECT c1 FROM t WHERE c1 = 10 FOR UPDATE; 会阻止其他事务插入、更新或删除t.c1值为10的数据行。

记录锁通常通过锁住索引记录来实现，即便一个mysql的table没有定义索引，在这种情况下InnoDB会创建一个隐藏的索引来用该索引来加记录锁。See Section 15.6.2.1, “Clustered and Secondary Indexes”.

阅读更多

经常使用公司的git仓库，同时也需要使用github，此时git的配置就会出问题。由于git配置的用户名和密码均是全局的，会导致如果使用github的配置如果不指定，就按照公司的git配置中的默认用户名提交。

解决办法，在github仓库中设置local配置

1
2
git config --local user.name xxx
git config --local user.email xxx@xxx.com
Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×